From the previous activity, we were able to create synthetic images of various shapes and patterns using Scilab. For this activity, we can proceed with the first step: to create a sample shape such as a rectangle. Incidentally, for the shapes from the previous activity, the background is black and the shape is white. These match the requirements of the edge detecting function of Scilab.
Triangles and circles were also made in Paint-- mainly to test the accuracy of the code for images made in Paint. At first, further editing of the produced rectangle image (from rectangle.bmp to rectangle2.bmp) was done in Paint as well, since the exported image also has a white border that has to be removed. Using imwrite in Scilab instead of export image allowed this step to be skipped.
The analytically known areas of the images are as follows:
rectangle = 230 x 138 pixels = 230*138 = 31,740 square pixels
circle = 200 x 200 pixels (radius is 100px) = pi*(r^2) = pi*(100^2) = 31,416 square pixels
triangle = 180 x 150 pixels = b*h/2 = 180*150/2 = 13,500 square pixels
The images were saved as rectangle2.bmp, circle.bmp, and triangle.bmp.
 |
| Fig. 1. Generated image of a rectangle (area = 31,740 square pixels). |
 |
| Fig. 2. Generated image of a circle (area = 31,416 square pixels). |
 |
| Fig. 3. Generated image of a triangle (area = 13,500 square pixels). |
The image was then loaded in Scilab using the following lines of code:
shape = imread('F:\rectangle2.bmp'); //rectangle2
shape2 = imread('F:\circle.bmp'); //circle
shape3 = imread('F:\triangle.bmp'); //triangle
The edge image was then obtained for each shape as follows:
shape = rgb2gray(shape);
edg = edge(shape, 'canny');
imshow(edg);
[y,x] = find(edg); //row then column which is why it is [y,x]
x0 = mean(x);
y0 = mean(y);
x = x-x0;
y = y-y0;
Note that rgb2gray(shape) was used since the .bmp images were not monochromatic, while the type of edge detection that was used was 'canny' since this allowed a unitary pixel width for the traced edges. Other types such as 'prewitt' were previously used but the errors obtained were higher than when 'canny' was used.
The edges obtained by 'canny' for the three shapes were as follows:
 |
| Fig. 4. Edge obtained for the rectangle. |
 |
| Fig. 5. Edge obtained for the circle. |
 |
| Fig. 6. Edge obtained for the triangle. |
The edge pixel coordinates of the shape were extracted using find(edg), noting that the order is reversed since row number is given by find() before the column number. The coordinates of the shape's center (x0,y0) were obtained by getting the mean() of all x and y values. The center coordinates were then subtracted from each of these values, to obtain coordinate values with (x0,y0) as the origin.
r = sqrt(x.^2 + y.^2);
theta = atan(y,x);
[theta2,k] = gsort(theta,'g','i');
for i = 1:length(k)
x2(i) = x(k(i));
y2(i) = y(k(i));
end
area = 0;
for j = 1:(length(k)-1)
area = area + x2(j)*y2(j+1) - y2(j)*x2(j+1);
end
calc_area = area/2;
The above code snippet performs the final steps in obtaining the area through Green's function. Each pair of edge pixel coordinates were used to obtain the corresponding r and theta in polar coordinates. The lists for theta, x, and y were then sorted using gsort(), with k containing the original positions of theta. This k served as the basis for the new lists x2 and y2, while theta2 was simply the new sorted theta by gsort(). Green's function states that the area of a shape given its edge coordinates are given by
where

are the number of pixels along the edge. This sums up the last five lines of the code snippet above.
Using the above code for all three shapes, I was able to obtain these values:
 |
| Fig. 7. Scilab output for the calculated area of the rectangle. |
 |
| Fig. 8. Scilab output for the calculated area of the circle. |
 |
| Fig. 9. Scilab output for the calculated area of the triangle. |
Overall, I would say that the areas were estimated pretty well. I assume that the larger deviations for the circle and the triangle were caused by the edge not being included in obtaining the area, since the calculated areas are consistently less than the analytic areas. The rough edges across the circle and the two diagonal sides of the triangle could have also played a part.
For the next part of the activity, we were instructed to use the code we just created on a real-world location. Using Google Maps, I was able to take an aerial screenshot of my house in Bay, Laguna:
 |
| Fig. 10. Screenshot of my house (red roof, topmost street) as seen in Google Maps. |
Using the above screenshot as the base image, I used Microsoft Paint to turn our lot into a white rectangle, with everything else in black.
 |
| Fig. 11. The screenshot with the entire lot replaced by a white rectangle on a black background. |
The above image (Fig. 5) I saved as a .bmp, and using the same code as before, I was able to obtain the area of our lot within that image in square pixels. In order to obtain real-world measurements, I used the small scale that was indicated by Google Maps in the bottom-right corner of the screenshot, which allowed a conversion from pixels to meters.
 |
| Fig. 12. The conversion scale of the Google Maps screenshot from 67 pixels to 10 meters. |
Using dimensional analysis, I was able to implement into the code the following:
//Note: 67 pixels = 10 meters from Google Maps screenshot
//Thus, 4489 square pixels = 100 square meters
calc_area = calc_area*100/4489;
Moreover, the My Maps feature of Google Maps allowed me to measure the exact area in hectares of any closed shape that I highlighted. In this case, I highlighted our lot:
 |
| Fig. 13. Screenshot of the My Maps feature giving 0.019 hectares as the area of the lot. |
Knowing the conversion from hectares to square meters, this gave me the following real-world data for comparison:
//1 hectare = 10000 square meters
//according to google maps: 0.019 hectares
//i.e. 190 square meters
gmaps_area = 190;
My output for Scilab ended up being:
 |
| Fig. 14. Edge obtained for the white rectangle representing the lot. |
 |
| Fig. 15. Scilab output for the calculated area of the lot. |
Comparing the two obtained values for calc_area and gmaps_area gave me a relatively small percent error. Thus, I am convinced that my code works for these purposes.
The last part of this activity required a scanner, and unfortunately, my research lab, SanD, had its scanner broken at the time of this activity. Thankfully, I was able to ask a classmate to scan my chosen flat image for me (thanks, Micholo!). This chosen personal item was my old Kansai Thru Pass. My classmate, Albert Yumol, advised me to scan a ruler beside the object as well.
 |
| Fig. 16. Scanned image of my Kansai Thru Pass. |
I realized that scanning the ruler was a bit redundant since, to double check the values provided by ImageJ, I had to measure the actual object with that same ruler by hand. However, it proved helpful in giving me a reliable scale from pixels to physical values (in this case, centimeters). This was 78.8406 pixels per centimeter, as seen below.
 |
| Fig. 17. ImageJ screenshot of the calibration step. |
When I looked for other details to measure in the Kansai Thru Pass, I was able to measure the length of the small "WELCOME TO KANSAI" blurb at the center of the card by hand, as well as the radius of the circle depicting Osaka. I measured around 2.60 centimeters length for "WELCOME TO KANSAI" and 1.05 centimeter radius for the Osaka circle. The latter value would mean a 3.46 square centimeter area for the Osaka circle.
When I went ahead in measuring these same details in the scanned image using ImageJ, I got the following data:
 |
| Fig. 17. ImageJ screenshot detailing the length of WELCOME TO KANSAI (2.587 centimeters). |
 |
| Fig. 18. ImageJ screenshot detailing the area of the Osaka circle (3.339 square centimeters). |
I would say that the discrepancies between 2.60 and 2.587 centimeters as well as 3.46 and 3.339 square centimeters are small enough for ImageJ's purpose. I think it could be attributed to the slight distortion caused by the thickness of the ruler while being scanned.
That would be the end of this long activity! All in all, it was fun, but rather long, in my opinion. Thank you to Gerald, Robbie, and Albert for helping me with coding.
Self-Evaluation: 10/10






 are the number of pixels along the edge. This sums up the last five lines of the code snippet above.
are the number of pixels along the edge. This sums up the last five lines of the code snippet above.












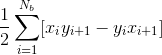
No comments:
Post a Comment