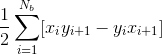AP186 Activity 5 Blog Report - Fourier Transform Model of Image Formation

For this activity, the first part involves steps that aid in familiarization with discrete FFT.

A white circle with black background was generated in an image of 128x128 dimensions. The radius of this circle in pixels can be calculated by multiplying 0.7 (as per the find(r<0.7) in the code) by the amount of pixels a linspace unit is: 64 pixels. This gives 44 pixels as the radius of the generated circle.

//circle
nx = 128; ny = 128; //defines the number of elements along x and y
x = linspace(-1,1,nx); //defines the range
y = linspace(-1,1,ny);
[X,Y] = ndgrid(x,y); //creates two 2-D arrays of x and y coordinates
r = sqrt(X.^2 + Y.^2); //note element-per-element squaring of X and Y
A = zeros (nx,ny);
A (find(r<0.7) ) = 1;
imwrite(A,'F:\AP186 - Activity 5 and 6\circ.bmp');

Fig. 1. White circle with black background with 128x128 dimensions and radius = 44 pixels.

This was opened using imread('F:\AP186 - Activity 5 and 6\circ.bmp'), and fft2(double(Igray)) was applied to the image. The intensity values were computed using uint8(255*abs(FIgray)/max(abs(FIgray))) and after checking with imshow(), the output was saved using imwrite().

Igray = imread('F:\AP186 - Activity 5 and 6\circ.bmp');
FIgray = fft2(double(Igray));
imwrite(uint8(255*abs(FIgray)/max(abs(FIgray))),'F:\imshow #1 (5.A, Step 3.).bmp');

Fig. 2. Discrete FFT of circle with radius = 44 pixels.

Notice that there are four quarter circles on the corners of Fig. 2. Applying fftshift(abs(FIgray)) on the image:

FSIgray = fftshift(abs(FIgray));
imwrite(uint8(255*abs(FSIgray)/ max(abs(FSIgray))),'F:\imshow #2 (5.A, Step 4.).bmp');

Fig. 3. Discrete FFT after FFT shift of circle with radius = 44 pixels.

The result is Fig. 2 but with the corner shapes combined into one small aperture at the center.

For a smaller circle radius (6 pixels) as a point of comparison, the following were obtained:

Fig. 4. White circle with radius = 6 pixels.

Fig. 5. Discrete FFT after FFT shift of circle with radius = 6 pixels.

Going back to the circle with 44 pixel radius, applying fft2(FIgray) to that in Fig. 3. again:

FI2gray = fft2(FIgray);
imwrite(uint8(255*abs(FIgray)/max(abs(FIgray))),'F:\imshow #3 (5.A, Step 5.).bmp');

The original image as in Fig. 1 is restored.

Performing the exact same steps for a 128x128 image of a letter "A" in Calibri font with font size 72, which was generated in MS Paint, produced the following images:

Fig. 6. Letter "A" in Calibri 72. 

Fig. 7. Discrete FFT of letter "A".

Fig. 8. Discrete FFT after FFT shift of letter "A". 

FT of a function is complex, and this can be proven by writing the following:
imwrite(mat2gray(real(fftshift(FIgray))),'F:\real2.bmp');
imwrite(mat2gray(imag(fftshift(FIgray))),'F:\imag2.bmp');

This results in the following for the shifted FFT of the circle with 6 pixel radius:

Fig. 9. Real part of the shifted FFT of circle with radius = 6 pixels.

Fig. 10. Imaginary part of the shifted FFT of circle with radius = 6 pixels. 

And it results in the following for the shifted FFT of letter "A":

Fig. 11. Real part of the shifted FFT of letter "A".

Fig. 12. Imaginary part of the shifted FFT of letter "A".

FT was applied to four more patterns: a sinusoid along x (corrugated roof), a simulated double slit, a square function, and a 2D Gaussian bell curve. The generated images and their corresponding shifted FFT results are below.

Fig. 13. Images (left) and their shifted FFT (right) for corrugated roof, double slit, square, and 2D Gaussian bell curve.

For the next part, which simulates an imaging device, a 128x128 image of the letters "VIP" was made in MS Paint, as shown below:

Fig. 14. Base "VIP" image for imaging device simulation.

Three aperture sizes were simulated by varying the radius of the circle image:

Fig. 15. Base apertures used for imaging device simulation.

Editing the aperture image used for each time, the code that was used three times was:

rgray=imread('F:\AP186 - Activity 5 and 6\mediumcircle.bmp');
a=imread('F:\AP186 - Activity 5 and 6\VIP2.bmp');
agray = rgb2gray(a);
Fr = fftshift(double(rgray));
Fa = fft2(double(agray));
FRA = Fr.*(Fa);
IRA = fft2(FRA); //inverse FFT
FImage = abs(IRA);
imwrite(uint8(255*abs(FImage)/max(abs(FImage))),'F:\imshow, edited (5.B, Step 4.).bmp');

What the above code does is that it first converts the MS Paint image of "VIP" to grayscale, then performs FFT shift on the aperture image, while the grayscale "VIP" has FFT performed on it. The product of their FFT is then obtained and FFT is performed on the product to get the inverse.

The results, respectively, were:

Fig. 16. Results for the three imaging device simulations.

From the above results, a smaller aperture lens shows a lower quality for the image, while a larger aperture lens shows a higher quality for the image.

For testing the template matching, the following sentence image was created:

Fig. 17. Base sentence image for template matching.

The other image that was used, which would be a component of the above image, was:

Fig. 18. Base component image for template matching.

The code that was used for this part was:

text=imread('F:\AP186 - Activity 5 and 6\raininspain.bmp')
a=imread('F:\AP186 - Activity 5 and 6\tiny_a.bmp')
Fa = fft2(double(a));
cFtext = conj(fft2(double(text)));
atext = Fa.*(cFtext);
Iatext = fft2(atext);
Iatext = fftshift(Iatext);
imshow(uint8(255*abs(Iatext)/max(abs(Iatext))));
imwrite(uint8(255*abs(Iatext)/max(abs(Iatext))),'F:\imshow, (5.C, Step 5.).bmp');

The steps performed by the above code are: the FT of the small A, the FT of the sentence image, the conjugate of this sentence image FT, and then an element-per-element multiplication of the small A FT and the sentence FT conjugate. The inverse FFT of the result is then shifted, and the output is as follows:

Fig. 19. Template matching result.

The result shows an "X looking mark with glowing white center" on all the places where the small A exists in the sentence. This is why it is called template matching, since the A component is matched with those in the base sentence image.

For the last part, which was edge detection using the convolution integral, a set of 3x3 matrix patterns of various types of edges was created. Each matrix has a total sum of zero. The matrix patterns created are as follows:

horizontal = [-1 -1 -1; 2 2 2; -1 -1 -1];

vertical = [-1 2 -1; -1 2 -1; -1 2 -1];

diagonal = [2 -1 -1; -1 2 -1; -1 -1 2];

spot = [-1 -1 -1; -1 8 -1; -1 -1 -1];

Using the VIP image in Fig. 14. once more, each of these matrix patterns were convoluted with the image, and the resulting image for each convolution was obtained. With credit to Robbie Esperanza for informing me of the best Scilab command to use for such matrices, I used a website (https://help.scilab.org/doc/5.5.2/en_US/conv2.html) as reference to create the following code:

a=imread('F:\AP186 - Activity 5 and 6\VIP2.bmp');
agray = rgb2gray(a);
C = conv2(double(agray),spot);
imwrite(uint8(255*C/max(C)),'F:\spot, (5.D, Step 2.).bmp');

The above code uses conv(2) to convolve the grayscale of the "VIP" image with the matrix used (either horizontal, vertical, diagonal, or spot). The resulting images are as follows:

Fig. 20. Resulting images for edge detection, using horizontal, vertical, diagonal, and spot matrix patterns, respectively.

The best edge detection method for the "VIP" image was through the spot matrix pattern. The other matrix patterns seem to only get the edges of the "VIP" image along the axis that they traverse.

Overall, the activity was not too difficult, but it gave its challenges. Much of the blogging part was delayed due to simultaneous requirements with other subjects, with research, as well as me having to recover from sickness, missing two days of class (although only one meeting for AP186) as a result.

Self-Evaluation: 9/10

Thank you to Albert Yumol and Robertson Esperanza for helping me throughout this activity.

AP186 Activity 4 Blog Report - Length and Area Estimation in Images

From the previous activity, we were able to create synthetic images of various shapes and patterns using Scilab. For this activity, we can proceed with the first step: to create a sample shape such as a rectangle. Incidentally, for the shapes from the previous activity, the background is black and the shape is white. These match the requirements of the edge detecting function of Scilab.

Triangles and circles were also made in Paint-- mainly to test the accuracy of the code for images made in Paint. At first, further editing of the produced rectangle image (from rectangle.bmp to rectangle2.bmp) was done in Paint as well, since the exported image also has a white border that has to be removed. Using imwrite in Scilab instead of export image allowed this step to be skipped.

The analytically known areas of the images are as follows:
rectangle = 230 x 138 pixels = 230*138 = 31,740 square pixels
circle = 200 x 200 pixels (radius is 100px) = pi*(r^2) = pi*(100^2) = 31,416 square pixels
triangle = 180 x 150 pixels = b*h/2 = 180*150/2 = 13,500 square pixels

The images were saved as rectangle2.bmp, circle.bmp, and triangle.bmp.

Fig. 1. Generated image of a rectangle (area = 31,740 square pixels).

Fig. 2. Generated image of a circle (area = 31,416 square pixels).

Fig. 3. Generated image of a triangle (area = 13,500 square pixels).

The image was then loaded in Scilab using the following lines of code:

shape = imread('F:\rectangle2.bmp'); //rectangle2
shape2 = imread('F:\circle.bmp'); //circle
shape3 = imread('F:\triangle.bmp'); //triangle

The edge image was then obtained for each shape as follows:

shape = rgb2gray(shape);
edg = edge(shape, 'canny');
imshow(edg);
[y,x] = find(edg); //row then column which is why it is [y,x]
x0 = mean(x);
y0 = mean(y);
x = x-x0;
y = y-y0; 

Note that rgb2gray(shape) was used since the .bmp images were not monochromatic, while the type of edge detection that was used was 'canny' since this allowed a unitary pixel width for the traced edges. Other types such as 'prewitt' were previously used but the errors obtained were higher than when 'canny' was used.

The edges obtained by 'canny' for the three shapes were as follows:

Fig. 4. Edge obtained for the rectangle.

Fig. 5. Edge obtained for the circle.

Fig. 6. Edge obtained for the triangle.

The edge pixel coordinates of the shape were extracted using find(edg), noting that the order is reversed since row number is given by find() before the column number. The coordinates of the shape's center (x0,y0) were obtained by getting the mean() of all x and y values. The center coordinates were then subtracted from each of these values, to obtain coordinate values with (x0,y0) as the origin.

r = sqrt(x.^2 + y.^2);
theta = atan(y,x);
[theta2,k] = gsort(theta,'g','i');
for i = 1:length(k)
    x2(i) = x(k(i));
    y2(i) = y(k(i));
end
area = 0;
for j = 1:(length(k)-1)
    area = area + x2(j)*y2(j+1) - y2(j)*x2(j+1);
end
calc_area = area/2;

The above code snippet performs the final steps in obtaining the area through Green's function. Each pair of edge pixel coordinates were used to obtain the corresponding r and theta in polar coordinates. The lists for theta, x, and y were then sorted using gsort(), with k containing the original positions of theta. This k served as the basis for the new lists x2 and y2, while theta2 was simply the new sorted theta by gsort(). Green's function states that the area of a shape given its edge coordinates are given by

whereare the number of pixels along the edge. This sums up the last five lines of the code snippet above.

Using the above code for all three shapes, I was able to obtain these values:

Fig. 7. Scilab output for the calculated area of the rectangle.

Fig. 8. Scilab output for the calculated area of the circle.

Fig. 9. Scilab output for the calculated area of the triangle.

Overall, I would say that the areas were estimated pretty well. I assume that the larger deviations for the circle and the triangle were caused by the edge not being included in obtaining the area, since the calculated areas are consistently less than the analytic areas. The rough edges across the circle and the two diagonal sides of the triangle could have also played a part.

For the next part of the activity, we were instructed to use the code we just created on a real-world location. Using Google Maps, I was able to take an aerial screenshot of my house in Bay, Laguna:

Fig. 10. Screenshot of my house (red roof, topmost street) as seen in Google Maps.

Using the above screenshot as the base image, I used Microsoft Paint to turn our lot into a white rectangle, with everything else in black.

Fig. 11. The screenshot with the entire lot replaced by a white rectangle on a black background.

The above image (Fig. 5) I saved as a .bmp, and using the same code as before, I was able to obtain the area of our lot within that image in square pixels. In order to obtain real-world measurements, I used the small scale that was indicated by Google Maps in the bottom-right corner of the screenshot, which allowed a conversion from pixels to meters.
 

Fig. 12. The conversion scale of the Google Maps screenshot from 67 pixels to 10 meters.

Using dimensional analysis, I was able to implement into the code the following:

//Note: 67 pixels = 10 meters from Google Maps screenshot
//Thus, 4489 square pixels = 100 square meters
calc_area = calc_area*100/4489;

Moreover, the My Maps feature of Google Maps allowed me to measure the exact area in hectares of any closed shape that I highlighted. In this case, I highlighted our lot:

Fig. 13. Screenshot of the My Maps feature giving 0.019 hectares as the area of the lot.

Knowing the conversion from hectares to square meters, this gave me the following real-world data for comparison:

//1 hectare = 10000 square meters
//according to google maps: 0.019 hectares
//i.e. 190 square meters
gmaps_area = 190;

My output for Scilab ended up being:

Fig. 14. Edge obtained for the white rectangle representing the lot.

Fig. 15. Scilab output for the calculated area of the lot.

Comparing the two obtained values for calc_area and gmaps_area gave me a relatively small percent error. Thus, I am convinced that my code works for these purposes.